BQ #4: Unit T Concept 3

Why is a "normal" tangent graph uphill, but a "normal" cotangent graph downhill?

Basically, a normal tangent graph is uphill because it is based on its asymptotes. They are located at pi/2 and 3pi/2. Furthermore, the quadrants are shown as positive, negative, positive, and negative (based on sin/cos). Cotangent is downhill because its asymptotes are located at 0 and pi. Because of where the asymptotes are located, it is downhill. The quadrants are positive, negative, positive, negative. The asymptotes are where sine and cosine are equal to 0 (making the ratio undefined).


                          Visual of Tangent 

(https://www.desmos.com/calculator)

As you can see, the colors represent the different quadrants (I,II,III,IV)

http://mathsm1m0838.edublogs.org/2009/08/01/the-tangent-graph/

Asymptotes at pi over 2 and 3pi over 2

  Visual of Cotangent

(https://www.desmos.com/calculator)

                                           

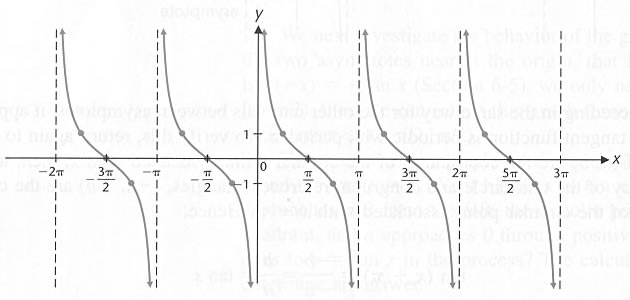http://www.oocities.org/mathnuts/TrigAGModule1-TrigFunctions/graphs-general-tan-cot-sec-csc-sec6p8/graphs-general-tan-cot-sec-csc.htm

Asymptotes at 0 radians and pi