A continuous function is predictable. It contains no breaks, no jumps, and no holes. It can be drawn without lifting a pencil. The intended height and the actual height of the graph are equal. On the other hand, a discontinuity has breaks, jumps, and holes. The intended height (limit) and actual height (value) are not equal to each other. The two families of discontinuity are removable and non-removable. The removable discontinuity is point discontinuity, in which there is a hole. The non-removable discontinuities are known as jump discontinuity, oscillating behavior, and infinite discontinuity. The limits don't exist in non-removable discontinuities. For jump discontinuity, the left and right limits are different, thus they don't exist. For oscillating behavior, it is very wiggly, so a limit cannot be determined because it does not approach a value. For a infinite asymptote, there is a vertical asymptote which means unbounded behavior.
.jpeg) |
| Removable and non-removable discontinuities (Please forgive my coffee stain, I think it's a sign that I need to cut back on coffee...) |
2. What is a limit? When does a limit exist? When does a limit does not exist? What is the difference between a limit and a value?
A limit is the intended height of a function. It exists at point discontinuities. Why? Because limits exists from when the left and right side matches, and meet, therefore they have the same intended height. An actual height is the value, while the intended height is it limit. A limit does not exist, however, at the three non-removable discontinuities. The right and left limits aren't the same. In an oscillating is wiggle and does not reach a single value, therefore it does not have a limit. An infinite discontinuity does not have a limit because it has unbounded behavior due to a vertical asymptote.
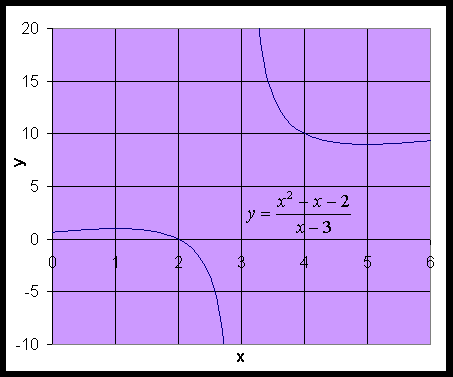 http://www-rohan.sdsu.edu/~jmahaffy/courses/s00a/math121/lectures/limits_cont_deriv/limits.html |
| Infinite discontinuity; unbounded behavior because of vertical asymptote Limit DNE |
 |
| http://tutorial.math.lamar.edu/Classes/CalcI/TheLimit.aspx Oscillating behavior; no limit because does not go to single value Limit DNE |
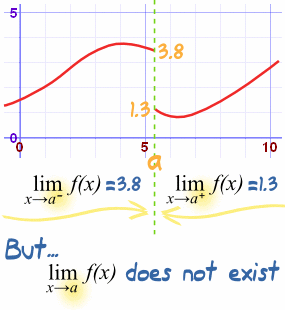 |
| http://www.mathsisfun.com/calculus/limits.html Jump discontinuty, limits from left and right don't match LIMIT DNE |
3. How do we evaluate limits numerically, graphically, and algebraically?
Numerically
For evaluating limits numerically, we use a table. The number that X is approaching in the middle is what we are using to find the limit. First, we need to subtract .1 from the given number and that would be in the first end on the table (beginning). We add .1 to the given number to get the end on the table (last). Then, basically the numbers will get smaller as we go towards the middle. Soon, it will be clear the numbers approach a certain value that will be our limit. The limit may or not be reached depending on the function though.
Graphically
To find a limit graphically, we basically use our fingers to see if the right and left side meet. If they don't meet, the limit does not exist. Below is a video that will show my explanation with a real graph for a visual. He also explains more into depth!
https://www.youtube.com/watch?v=aVcqrDFcaCA
Algebraically
To find limits algebraically, there are three different ways. First is direct substitution. In direct substitution, you plug in the given number and see what you get. If you get 0, a numerical answer, undefined (limit DNE), then you are done. If you get 0/0, that is an indeterminate form, and you have to use another method! The next method is factoring method. You have to basically factor the numerator and denominator. After, cancel common terms, then plug in the given into the equation that is left. The next method is conjugate method, where you rationalize depending where the radical is in the numerator or denominator. You take the conjugate of what has a radical- either in the numerator or denominator. Then you multiply the entire fraction by the conjugate. Remember, you want to try direct substitution first because you don't want to go through a huge hassle if you can already get an answer using it. That is just a cheese bucket move, and no one wants to be called a cheese bucket because of this silly mistake!
Sources
https://www.youtube.com/watch?v=aVcqrDFcaCA
http://tutorial.math.lamar.edu/Classes/CalcI/TheLimit.aspx
http://www.mathsisfun.com/calculus/limits.html
http://www.rohan.sdsu.edu/~jmahaffy/courses/s00a/math121/lectures/limits_cont_deriv/limits.html
SSS packet
.jpeg)